이번 포스팅에서는 Gradient Descent에 대해 말 해보려고 한다.
모델 학습 (Training) => 모델 변수 값을 정하는 행위 라고 말할 수 있다.
=> 최적화 이론이라는 것이다.
알고있는 정도와 원하는 정보가 있으면 그 값을 에측하는 것이다.
만약, 정해진 형식이 있다면 사실 이를 예측할 필요가 없다.

하지만 우리가 원하는 것은 예측을 하여 그 예측 값을 최소화 시키는 것이다.
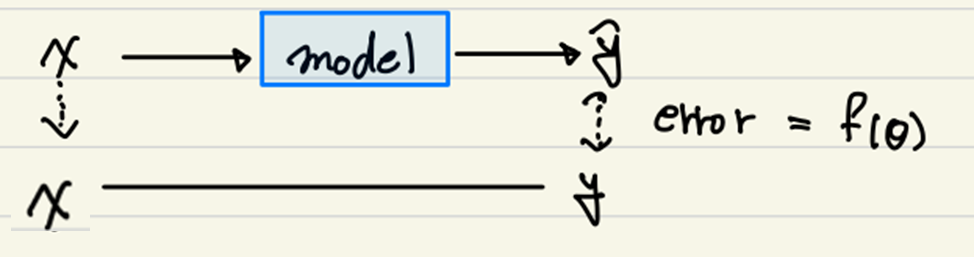
여기서 x의 값이 y라는 사실을 알고 있다고 하자.
우리는 x를 model안에 집어 넣어서 예측값인 y.pred값을 model로 부터 얻어낸다.
이를 우리는 loss라고 한다.
그렇다면 M/L(Machine Learning)의 Training 목표는 무엇일까?
"Training의 목표 => min(F(θ))가 되는 θ찾기" 라고 볼 수 있다.
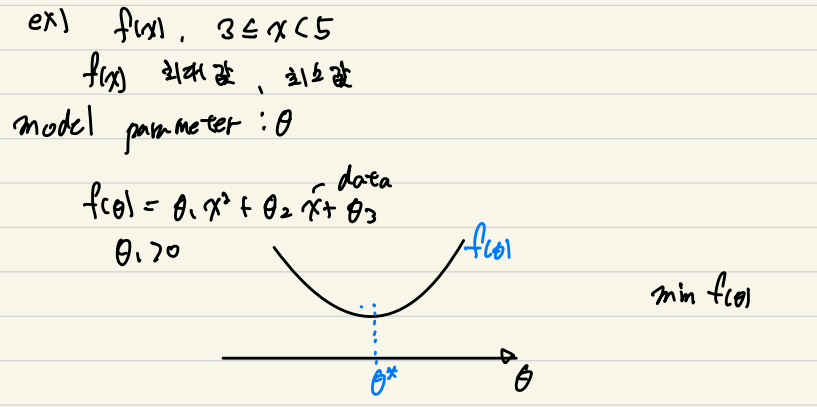
위의 그림은 2차 함수의 예시이다.
단순히 기울기가 0이 되는 계산 방법 말고 Gradident Descent 방법을 적용해 보려고 한다.

이는 현재의 값인 θ0에 작은 값을 더하거나 뺴서 θ*을 만드는 방법이다.
(θ의 값이 목표치보다 크면 작게 만드고, 작으면 크게 만든다._loss값을 통해 결정)
작은 값은 learning rate의 비율을 통해 결정되는데 자신이 개발하고자 하는 모델에 따라 알맞게 쓰면 된다.
(lr = 0.001 을 주로 쓰기는 한다...)
그렇다면 당연히 learning rate가 올라갈 수록 수렴이 빨라 지지만, θ* 주변에서 진동하며 끝내 θ*에 도달하지 못할 수 있다.
learning rate가 낮아질 수록 수렴이 늦어지지만. 비교적 θ*에 근접해질 수 있다.
그렇다면 왜 G/D를 쓰는가?
M/L은 우리가 생각 할 수 있는 그런 2차원의 그래프가 거의 나오지 않는다.
수천가지의 차원 그래프가 나오게 되는데, 이를 계산하기 위해서는 너무나도 많은 계산량이 필요하기 때문이다.
이에 우리는 G/D를 택하게 된 것이다.
정리하자면,,,

하지만 문제점 또한 존재하게 된다.
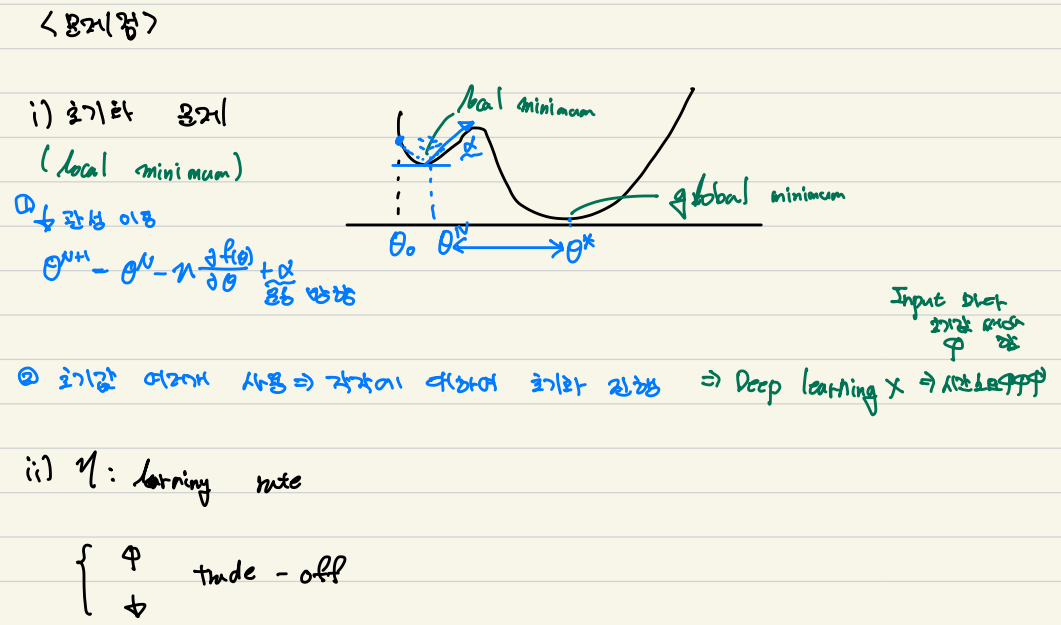
1. local minimum 문제 : 최소값이 아닌 다른 곳에 빠지게 되는 문제이다. 글로 설명이 어려우니 밑에 그림을 봐주면 좋을 것 같다.
2. learning rate : trade off의 관계이다.
'michine learning(미친러닝) > ML 공부' 카테고리의 다른 글
| (ML) Confusion Matrix _ TP,FP,FN,TN (0) | 2023.07.13 |
|---|---|
| (ML) 활성화 함수(Activation Function) _ 개념편 (0) | 2023.07.07 |
| (ML) 인공지능이란 무엇인가? (0) | 2023.07.07 |
| (ML) 활성화 함수(Activation Function) _ 실전편 (0) | 2023.07.06 |
| (ML) MBConv _ Depth-wise Convolution (0) | 2023.07.05 |
댓글